5 juin 202328 min de lecture

61. La Lune, Mesure de Toute Chose

Dernière mise à jour : 13 janv.

Revellers, Blue stone and moon, Photograph by Andrew Dunn, 20 June 2005.Wikimedia Commons

Protagoras a dit "L'homme est la mesure de toutes choses". Peut-être voulait-il dire que chacun doit percevoir, expérimenter et comprendre les choses par lui-même. Peut-être voulait-il nous rappeler qu'il n'y a pas de vérité objective. Ou peut-être voulait-il dire que les systèmes de mesure dépendent des proportions du corps humain. Ou peut-être voulait-il dire que les gens façonnent le monde dans lequel nous vivons, pas le destin ou les dieux. Lorsque nous essayons de donner forme et ordre au monde, le basons-nous simplement sur des abstractions, comme le nombre ? Ou l'avons-nous historiquement basé sur les choses mêmes qui nous gouvernent, qui sont bien au-delà de notre contrôle, comme le soleil et la lune, et peut-être aussi le destin et les dieux aussi ?

Il semble paradoxal que nous puissions concevoir des systèmes de mesure et de prédiction dans lesquels ancrer nos expériences du monde sur le soleil et la lune. Ces deux corps célestes peuvent être cycliques dans leurs activités, ce qui les rend aptes à marquer le passage du temps, mais ce sont aussi les choses mêmes sur lesquelles nous n'avons aucun pouvoir en tant qu'humains et dont nous dépendons tellement. Nous les conaissons à travers le climat et les saisons, la lumière et l'obscurité, les marées, et même nos états d'esprit. Dans un premier temps, le soleil nous donne le jour et l'année comme unités de temps, et la lune nous donne le mois. En tant que parties du calendrier, ces périodes de temps sont des blocs de construction essentiels. De nombreux calendriers anciens sont lunaires, ou bien combinent les modèles du soleil et de la lune (luni-solaire), et ainsi la lune semble avoir toujours eu une place prépondérante pour marquer le passage du temps. La lune est-elle la mesure de toutes choses ?

Le mot latin pour mesure est mensura, et le verbe mesurer est metiri. Notre mot pour mesure est également lié à d'autres langues, telles que le sanskrit mati, le vieux persan ma- et le grec metron, qui signifie également mesure. Le mot "lune" n'est pas seulement lié au mot "mesure", mais est également similaire dans de nombreuses traditions linguistiques différentes. En moyen anglais, c'est mone, en vieil anglais mona, en vieux saxon et en vieux haut allemand c'est mano, en vieux frison mona, en vieux norrois mani, en danois maane, en néerlandais maan, en allemand mond, en sanskrit masah, en persan mah, en grec mene "lune", ". Le mot latin mensis, signifiant "mois" dérive également de cette tradition. Et de nombreuses autres langues ont des mots similaires pour la lune et le mois, comme le lituanien, avec mėnesis « lune, mois » vieil irlandais mi, gallois mis, breton miz, tous signifiant mois. Le son commun à la plupart de ces mots est "me", ou "ma", ou "mo", une racine étymologique qui signifie "mesure".

La lune est également liée à l'intelligence et à la connaissance dans plusieurs religions anciennes. Par exemple, Manasvini, une déesse hindoue associée à la vertu, on dit aussi que l'intelligence est la mère de la lune. Elle est liée par son nom et par ses associations lunaires à la déesse romaine Minerve, la plus sage de tous les dieux et déesses. Le nom de Minerve est dérivé d'une déesse plus ancienne appelée Meneswā ou Menes-wo, signifiant « celle qui se souvient », « celle qui sait » ou « celle qui mesure ».

Le mouvement de la lune est une ancienne mesure du temps très répandue. Il n'est pas surprenant que les cycles de la lune soient liés à nos mois calendaires, qui ont été légèrement allongés pour s'adapter à une année solaire, mais il semble que la lune ait également été comprise comme une source de connaissances et même d'intelligence. Est-il possible que la lune ait autrefois fourni la base d'un système de connaissance et de mesure, conçu non seulement pour les calendriers, mais pour toutes choses ? Une façon de le savoir est de regarder les sites antiques et de voir si les nombres associés aux cycles de la lune s'y produisent assez régulièrement pour pouvoir établir un lien entre la lune et la mesure du temps et de l'espace.

Nombres lunaires

Alors, quels nombres sont qualifiés de lunaires ? Il y a le nombre de jours dans un mois lunaire moyen, 29,53059. Il y a le nombre de jours dans un mois draconique, 27,2122, et l'année draconique ou éclipse est de 346,620075883 jours. La période de rotation sidérale de la lune est de 27,321661 jours. Il y a le nombre de mois lunaires dans un cycle Metonic de 19 ans, 235, ainsi que le nombre de mois lunaires dans un cycle de 8 ans, 99. D'autres cycles incluent une période de 223 mois lunaires. Il y a aussi 12 et 13, le nombre de mois possibles dans une année solaire, et le nombre moyen par an est 365,242199 / 29,53059 = 12,3682662. Le nombre de jours de différence entre les années solaires et lunaires est de 10,875119. Ensuite, il y a 7 et 4, le nombre de jours dans une semaine et de semaines dans un mois. Et il y a d'autres nombres moins évidents, comme 47. 309 lunaisons sont 25 ans de 365 jours, un cycle dont les Égyptiens étaient friands. Comme Guyla Priskin l'a observé, 309 + 309 = 618, c'est 1000 phi. Les nombres qui dépendent déjà d'un système de mesure, comme les dimensions de la lune, sont également importants. 1080 en est un exemple, avec un rayon équatorial de 1 738,1 km, soit 1 080,005 milles. Peut-être est-ce un peu fou d'imaginer que le mile a été conçu pour pouvoir exprimer le rayon de la lune avec un nombre qui était déjà centralà une manière sophistiquée de calculer le mouvement de la lune. Pourquoi 1080 est-il lunaire ?

Le calendrier hébreu

Hebrew Calendar (Luach), Printed by I. Lehrberger u. Comp., Rödelheim. In the collection of the Jewish Museum of Switzerland, Wikimedia commons

Le nombre 1080 est également au centre du calendrier hébreu. Dans ses recherches approfondies sur le calendrier hébreu, Irv Bromberg explique que le nombre 1080 était utilisé pour diviser le temps, en particulier l'heure, afin de permettre d'exprimer la durée d'une lunaison sans utiliser de fraction. C'est assez compliqué, mais j'ai cité l'explication d'Irv Bromberg pour illustrer la complexité et la sophistication de son ancien calendrier.

La durée d'une partie ou chelek équivaut au grain d'orge babylonien antérieur, la plus petite unité de temps babylonienne, qui était de 1/72 de degré de temps. Le degré de temps était la principale unité de temps babylonienne, correspondant au temps nécessaire pour un degré de mouvement du Soleil à travers le méridien = 1/360 d'un jour solaire = 1440 minutes par jour/360 degrés de temps par jour = 4 minutes par temps degré. Ainsi 4 minutes divisées par 72 = 1/18 de minute = 1 chelek. Le degré de temps est également presque égal à la différence de durée entre le jour solaire et le jour sidéral, qui, à l'époque actuelle, s'élève à environ 3 minutes et 55,9 secondes. Le doigt babylonien était de 6 grains d'orge = 1/12 de degré de temps = 1/3 de minute = 20 secondes de temps. La coudée était de 180 grains d'orge = 5/2 degrés de temps = 10 minutes de temps. L'heure elle-même, correspondant à 15 degrés de temps, était une unité de temps séleucide qui provenait probablement d'Égypte. Le beru babylonien ou heure double, correspondait à 30 degrés de temps. Le mois synodique moyen dans les unités de temps babyloniennes était de 29 jours, 6 heures doubles, 11 degrés de temps et 1 grain d'orge.

Si nous divisons le numérateur 13753 par 1080 pour séparer le nombre d'heures des parties restantes nous obtenons :

étage (13753/1080) et reste (13753 mod 1080) = 12 heures, avec reste 793 pièces

Les 793 parties restantes correspondent à 2/3 d'heure + 73 parties = 44 minutes + 1 partie = 44 + 1/18 minutes. C'est exactement une partie supérieure à 2/3 + 1/15 = 11/15 d'heure.

Dans une moitié du cycle molad complet, il y a 25920/2 = 12960 mois, donc chaque cycle complet contient un excès de 13753 – 12960 = 793 mois complets, ce qui correspond exactement aux 793 parties restantes au-delà de 29 + 1/2 jours . De même, il y a un déficit de 12960 – 12167 = 793 mois déficients, puisque ce nombre de mois autrement déficients est complété à chaque cycle complet.

Par conséquent, l'intervalle de molad traditionnel est de 29 jours, 12 heures, 793 parties. La durée de l'intervalle molad est essentielle à l'arithmétique du calendrier hébreu traditionnel et doit être exprimée en utilisant uniquement des nombres entiers et des fractions appropriées afin que toute date puisse être calculée exactement et sans ambiguïté. (Longtemps après avoir publié cette page web, j'ai appris que le Gaon de Vilna expliquait de la même manière que seule la division des heures en 1080 parties permet d'exprimer la durée de la lunaison sans utiliser de fraction, voir le commentaire de Kol Eliyahu sur le Talmud Bavli traité de Rosh HaShanah page 25a.) Le calcul exact d'un moment molad n'est pas aussi compliqué que cela puisse paraître, car, comme l'a souligné Rambam (chapitre 6) les 29 jours comprennent 4 semaines plus 1 jour restant, donc si l'on connaît déjà le molad moment pour un mois donné, le moment molad du mois suivant sera de 4 semaines, 1 jour, 12 heures et 793 parties plus tard. De même, si l'on connaît le moment molad de Tichri d'une année donnée (utilisé pour déterminer la date de Roch Hachana), alors le prochain molad de Tichri après une année non bissextile sera de 12 × (4 semaines, 1 jour, 12 heures , et 793 parties) = 354 jours et 9516 parties = 50 semaines, 4 jours, 8 heures et 876 parties (73/90 d'une heure = 48+2/3 minutes = 48 minutes et 40 secondes) plus tard, et après un l'année bissextile sera 13 × (4 semaines, 1 jour, 12 heures et 793 parties) = 383 jours et 23269 parties = 54 semaines, 5 jours, 21 heures et 589 parties (32 minutes et 13 parties) plus tard. (3)

Le nombre 54 est la moitié de 108, et ces nombres sont également associés au cycle précessionnel et à l'astronomie indienne. Il est donc intéressant de voir une période de 54 semaines ici.

Gizeh

Great Pyramid of Giza and Sphinx, Photo by Mohamed Ahmed Yousry, Wikimedia Commons

Un bon endroit pour commencer à chercher des nombres lunaires dans les bâtiments du monde antique est Gizeh, car il a été mesuré avec précision et est évidemment l'œuvre d'architectes et de constructeurs hautement qualifiés et sophistiqués. Si les trois plus grandes pyramides de Gizeh sont considérées dans un rectangle défini par leurs positions relatives, les dimensions de ce rectangle révèlent des nombres lunaires.

Ce rectangle est positionné dans l'axe nord-sud. Flinders Petrie donne 29 227,1998 pouces ou 742,370876 m (W-E) et 35 713,2 pouces ou 907,115281 m (N-S) comme dimensions. Cela pourrait être interprété comme suit : la largeur ouest-est étant de 29,53059 x12 x 4 x 0.5237226 = 742.3602 m, encodant 4 années lunaires en coudées, ou comme 365,242199 x 80 = 29219,38, encodant 80 années solaires en pouces. Il y a un léger écart, car cela équivaut en fait à 80,02027 ans.

Ce décalage est intéressant. 80 multiplié par 365,242199 donne 29 219,37592, et cela, divisé par le nombre de jours en 4 années lunaires, 1 417,46832, donne 0.5235899 m. Comme mesure en pouces, c'est un peu plus court que les 0.5237226 m que nous trouvons en divisant la largeur par 4 années lunaires : 0.52373 m. Le rapport entre ces deux longueurs de coudée serait de 1,00026777. Comme mesure en pouces, 20.613777, ce dernier chiffre serait donner une correspondance précise entre les années solaires 80 et les années lunaires 4. La largeur, selon Flinders Petrie, est de 29 227.1998 pouces, et divisée par 80 donne 365.3399975, mais si nous divisons cela par le rapport entre les deux longueurs de coudée, nous obtenons beaucoup plus correspondance précise entre la longueur en pouces et la longueur d'une année solaire : 365,242197 pouces.

Si la même mesure linéaire peut produire 80 années solaires en pouces ou 4 années lunaires en coudées, qu'est-ce que cela peut nous dire sur la relation entre les pouces et les coudées plus généralement ? Le rapport entre 80 années solaires et 4 années lunaires est de 20,613777. Bien qu'un peu petit, cela pourrait servir de mesure ou de coudée égyptienne en pouces. Divisé par pi et 10, cela nous donne 0,656157, qui pourrait être une mesure ou le shusi en pouces, qui ensuite multiplié par 10/9 donne 0,7290362, qui pourrait être une mesure du chiffre égyptien en pouces. Le rapport de 80 années solaires et 4 années lunaires est en effet parfaitement représentatif du rapport entre 20 années solaires et une année lunaire : 365,242199 x 20 / (12 x 29,53059) = 20,613777, correspondant a une coudée de 0.528057 m.

La longueur nord-sud du rectangle pourrait peut-être être comprise comme 346,620076 x 5 x 0.523405 = 907.1135777 m, encodant cinq années draconiques en coudées, mais avec une coudée beaucoup plus courte. Une autre option pourrait être de voir cela comme 1000 x √3 coudées de 0.52373 m, trouvées dans la largeur. 1 année draconique est de 346,620076 jours, et donc 5 années draconiques sont de 1733,10038, ce qui est très proche de √3x1000, et 4 années lunaires en jours sont raisonnablement proches de √2x1000 jours. La théorie √2:√3 avancée par John Legon, définissant le rectangle comme √2:√3, est très intrigante. La longueur, que John Legon associe à √3, suggère que ce nombre irrationnel aurait pu être autrefois lié à un période de cinq années draconiennes. Une autre interprétation des dimensions de ce rectangle a été proposée par Manu Seyfzadeh comme 9 x 11 (communication personnelle). C'est un meilleur ajustement. Une interprétation possible de ce rapport est qu'il produit une grille de 99 carrés, 99 étant le nombre de mois lunaires en huit années solaires, ce qui correspond également à un cycle de Vénus.

Le cycle de 99 mois lunaires, qui dure 8 années solaires, définit le rectangle de Gizeh. La largeur du rectangle peut être interprétée à la fois comme 80 années solaires en pouces et 4 années lunaires en coudées de 20,61901 pouces. Le rapport entre 80 années solaires et 4 années lunaires représente le rapport entre 20 années solaires et une seule année lunaire : 365,242199 x 20 / (12 x 29,53059) = 20,613777. Peut-être que le rapport année solaire / année lunaire a simplement été appliqué au cycle de 8 ans, puis multiplié par 10, car 80 années solaires sont 10 cycles de Vénus, 990 lunaisons, à une approximation très proche.

D'autres nombres lunaires peuvent être trouvés dans la disposition générale des pyramides de Gizeh, par exemple entre la Grande pyramide et celle de Menkaure.

Quelle pourrait être la signification de 3 000 lunaisons ? Le chiffre traditionnel donné à la longueur d'un cycle de précession en années est de 25 920. La relation entre les années solaires et lunaires peut être exprimée comme pi multiplié par la longueur d'un cycle précessionnel divisé par 30 000. Ainsi, avec 22/7 pour pi, et le nombre 10,875119 comme différence en jours entre douze mois lunaires et une année solaire, 3 000 x 10 x 29,5306 / 10,875119 x 7/22 = 25 919,992. La durée d'une lunaison a progressivement diminué au cours des derniers millénaires, et la durée d'une année solaire a légèrement augmenté, donc ce nombre 10,87512 peut ne pas correspondre exactement au nombre utilisé il y a longtemps par les astronomes, mais doit être proche. Cette équation était peut-être connue il y a longtemps.

La largeur du rectangle de Gizeh peut être considérée en terme de mois lunaire, parce que 295,3059 x 11 x 9 pouces donne un chiffre assez proche de la largeur du rectangle de Gizeh. Et 295,3059 x 11 x 11 correspond raisonnablement bien à la longueur du rectangle de Gizeh, le premier chiffre étant environ 8 pouces plus long que les mesures de Flinders Petrie, et le second environ 18.8 pouces plus long.

Dennis Payne a également constaté que si l'on prend la mesure entre la troisième pyramide et la Grande pyramide, centre à centre, on obtient une mesure de 36 864 pouces. En utilisant une mesure de 9071,8 pouces pour le côté de la Grande Pyramide, nous pouvons diviser cela par 36 864, puis multiplier par 120, ce qui donne 29,5306.

Un autre exemple de code lunaire est en pouces, dans les dimensions de la Grande Pyramide elle-même. La hauteur est donnée comme 146.7104 m (5776 pouces anglais) par Flinders Petrie, et cela pourrait être interprété comme √(365,242199 / 354,36708 x 20 000 000 x Phi) = 5775,267, impliquant les années solaires et lunaires en jours et le nombre d'or. La pente de la pyramide devient alors √(365,242199 / 354,36708 x 20 000 000 x Phi²) = 7 346,26086 pouces, et la base devient √(365,242199 / 354,36708 x 10 000 000 x Phi x π). Cela signifie que les dimensions principales de l'extérieur de la pyramide pourraient être compris comme l'expression du rapport entre l'année solaire et lunaire, en pouces anglais.

Un côté de la deuxième pyramide peut être interprété comme 411 coudées, 411 étant un cycle lunaire en jours.

Une corrélation lunaire surprenante apparaît lorsqu'un calendrier de 52 semaines, qui appartient autant aux cycles des Mayas et des Aztèques qu'aux calendriers modernes, est appliqué à la base de la Grande Pyramide. Si nous prenons les 9068,8 pouces par côté moyen de la Grande Pyramide, selon Flinders Petrie, et le multiplions par 4 pour obtenir un périmètre de base de 36 275,2 pouces. Converti en mètres, cela donne 921,39008 m. Divisé par 52, cela donne 17,71904. Multiplié par 10, c'est le nombre de jours dans 6 mois lunaires. Divisé par 6, ce chiffre donne un mois lunaire de 29,5317333, ce qui est très proche de l'estimation actuelle de 29,53059. Ce serait une correspondance parfaite si nous réduisions légèrement le chiffre du côté de base moyen à 9068,448888 pouces, ce qui est bien dans les paramètres de Flinders Petrie. Si le périmètre de la Grande Pyramide correspond à 6/10 mois lunaires, en mètres modernes, alors un côté peut être considéré comme 29,53059 jours, une lunaison, multiplié par le nombre de semaines de 7 jours dans une année civile, 52, multiplié par 3/20, équivaut à 230,338602 mètres ou 9068,448888 pouces. Par coïncidence, 230,34 est le nombre de pouces à la hauteur de la chambre du roi, comme l'a souligné Dennis Payne, et donc les mêmes associations lunaires peuvent y être faites, mais en pouces au lieu de mètres. Stephen Dail a observé que Petrie notait l'utilisation d'une coudée de 20,607 pouces dans la hauteur de la Chambre du Roi, et que cette coudée correspond à la racine cubique de 8750, qui, multipliée par √125, donne 230,39326 pouces.

Le schéma ci-dessous montre une compréhension possible des dimensions de la grande pyramide en termes de rapport entre les années solaires et lunaires, combiné avec le nombre d'or, Phi.

Encore un autre exemple est dans la disposition relative des deux plus grandes pyramides. La distance N-S entre leurs faces sud est de 346,32 mètres et la distance N-S entre leurs centres est de 353,68 mètres.

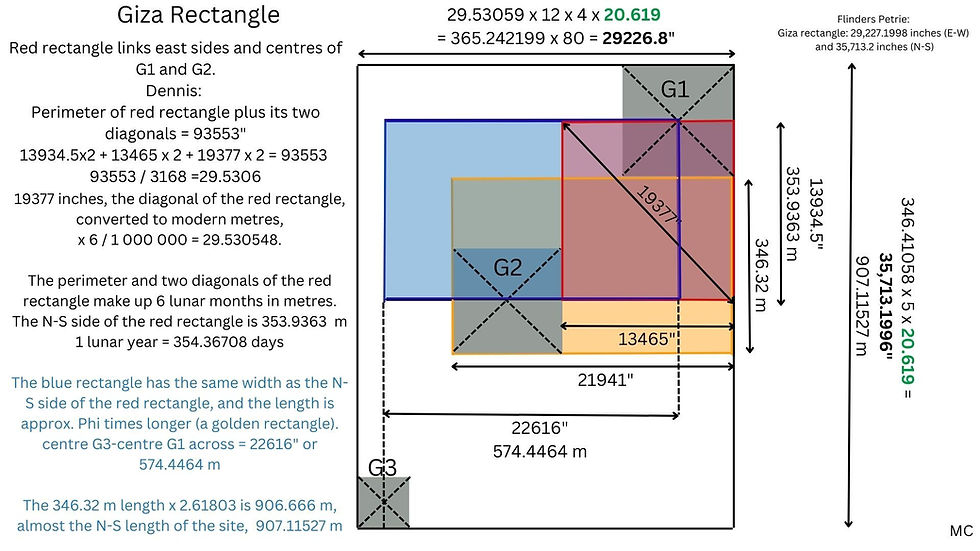
Le schéma ci-dessous est une illustration d'une découverte faite par Jim Wakefield en regardant les dimensions d'une autre pyramide, la pyramide de verre du Louvre.

Ce diagramme est une illustration de la connexion du mètre et du pouce en fonction du soleil et de la lune. Et si le mètre était compris comme une expression du mois lunaire en pouces, multiplié par un facteur ? Peut-être que le mètre pourrait être considéré comme 29,53059 x 4/3 pouces, ou 47 x 4/15 x π pouces (1.00011555 m) ? Cela donnerait une valeur pour le mètre de 39,374628 pouces, ce qui n'est pas loin de 39,375". Le mètre, exprimé en pouces, est proche du rapport entre l'année solaire et le mois lunaire, x 10/π. Jim Wakefield a trouvé que 9 mètres x 39,375 est 354,375.

Ce diagramme montre comment le nombre de jours d'un mois lunaire peut être élevé au carré et multiplié par pi et 25, pour produire le nombre de jours d'une période métonique de 19 ans. Le nombre de mois d'une période métonique peut être obtenu en multipliant le nombre de jours d'un mois lunaire par 25 et en divisant par pi. En conséquence, on peut exprimer pi lui-même en termes lunaires, par exemple 29,53059 x 25 / 235 ou 29,53059 x 29,53059 x 25 / (365,242199 x 19). On pourrait interpréter la longueur d'un côté de la Grande Pyramide de Gizeh, donnée par Flinders Petrie comme 9068,8 pouces, comme 29,53059 x 29,53059 x 4/3 x 78/10 = 9069,38 pouces, soit un peu plus d'un pouce sur 29,53059 x 78/10 mètres (modernes). En fait, 29,53059 x 4/3 = 39,3812 pouces, ce qui équivaut à un peu plus d'un mètre moderne en pouces, soit 39,3700787402 pouces.

Des exemples brillants de la lune à Gizeh et d'autres sites antiques ont été trouvés par des chercheurs tels que Jim Wakefield et Dennis Payne, comme ci-dessous. Dennis Payne a trouvé des connexions lunaires étonnantes, dont beaucoup à Gizeh. Ci-dessous, trois images créées par Dennis, publiées sur Academia, dans lesquelles il explique les connexions qu'il a trouvées, à Gizeh. les schémas parlent d'eux-mêmes. Ce travail est d'une précision absolue, et propose de repenser totalement la façon dont nous appréhendons ce site antique.

Le premier diagramme présente le nombre 47. Ce nombre est exploré plus loin ci-dessous.

Dans le diagramme ci-dessous, Dennis montre une corrélation lunaire géométrique dans la distance entre les deux plus grandes pyramides de Gizeh. La diagonale du rectangle rouge est de 19377 pouces. Converti en mètres modernes, multiplié par 6 et divisé par 100, cela donne 29,530548 m. Ainsi, le périmètre et les deux diagonales du rectangle rouge forment 6 mois lunaires en mètres. Le nombre 254 relie le mètre au pouce.

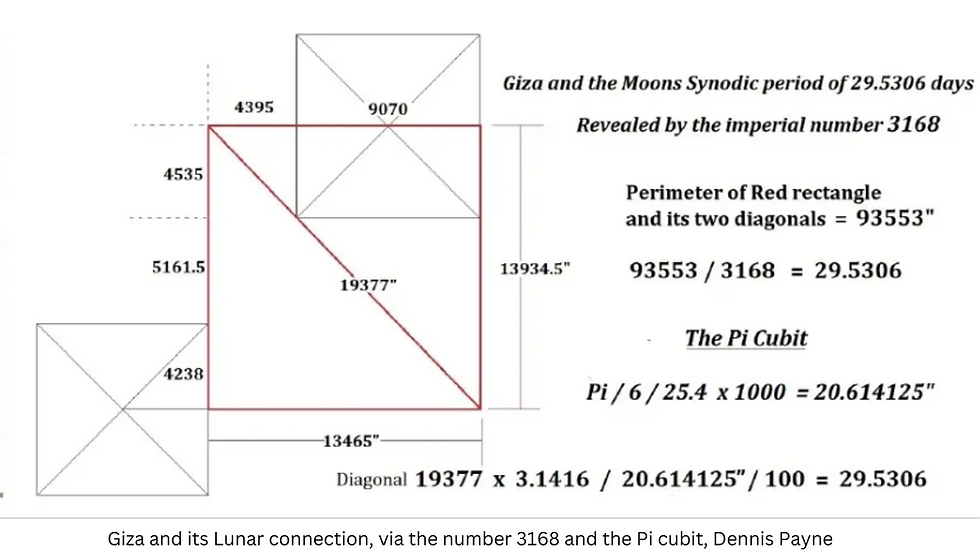
Le triangle ci-dessous est particulièrement impressionnant et fait apparaître le nombre 29,53059² observé à l'époque métonique, ci-dessus.

Comme Dennis a souligné, "si nous acceptons la prémisse de transformer des nombres constants en unités de mesure linéaires, alors il faut accepter qu'ils avaient une unité équivalente en longueur à notre pouce moderne."

John Michell, dans son livre Ancient Metrology, utilise un rapport pour convertir la coudée commune de Samos en coudée royale égyptienne qui peut être lunaire, et ce rapport est également utilisé par Jim Alison et Stephen Dail. La distance Terre/Lune varie entre 407 000 km (apogée) et 357 000 km (périgée). Le rapport entre les chiffres du périgée et de l'apogée peut être légèrement simplifié à 22/25. Un pied de 12 pouces x 126/125 = 12,096, et c'est le pied de Samos. Ce pied de Samos multiplié par 1,5 pour faire la coudée, puis par ce rapport de 25/22 donne 20,61818 pouces ou 0.523701818 m, ce qui est une valeur possible pour la coudée royale égyptienne. Avec cette coudée, le côté de la base de la Grande Pyramide, pris à 9072 pouces ou 230.4288 m, mesure exactement 440 coudées.

John Michell a également proposé cette équation bien connue : le rayon (en nombres canoniques, c'est-a-dire multiples de 9, 25920, 54, 108, etc) de la terre, 3960 milles, plus le rayon (canonique) de la lune, 1080 milles, font 5040 milles, 5040 étant un nombre important pour Platon, dans la République, et égal à 7 ! (ce qui est 1 x 2 x 3 x 4 x 5 x 6 x 7). Pris comme le rayon d'un cercle, ce 5040 multiplié par 2 et 22/7 pour pi, donne une circonférence de 31680 milles, et c'est la encore un autre nombre important, et qui est égal à 4 diamètres terrestres de 7920 milles.

Un examen attentif des dimensions des pyramides et de leur position relative révèle qu'une simple progression à partir de 10 000 pouces peut expliquer bon nombre des dimensions, comme l'illustre ce diagramme. En particulier, le nombre de jours d'une lunaison, 29,53059, est un facteur qui relie différentes sections du plan de Gizeh, avec pi et la racine carrée de trois. En fait, le nombre de lunaisons dans une année, en moyenne, peut être approximé par cette fraction : π x √3 x 100 / 44 = 12,36681. De sorte que même pi et la racine carrée de trois peuvent être considérés comme lunaires. Les 440 coudées présentes dans la base moyenne de la Grande Pyramide peuvent également être liées à cette équation. Et le côté moyen de la base de la Grande Pyramide peut être compris comme π x √3 x 10 000 / 6 = 9068,9968 pouces.

Stonehenge

Voici un diagramme d'une des découvertes de Jim Wakefield à Stonehenge :

Jim montre que les dimensions du cercle de Sarsen peuvent être reliées au cycle lunaire.

Le diamètre à Stonehenge est proche de la circonférence à Stanton Drew, où une comparaison similaire avec la lune peut donc être faite.

Teotihuacán

Dennis Payne a également trouvé des connexions lunaires intrigantes à Teotihuacan. Le circuit autour de la plate-forme des Citadelles est de 4677,646 pieds, ce qui, divisé par 1584, donne 29,53059. En pouces, cela devient 316,8 x 6 x 29,53059 ou 1900,8 x 29,53059. 19008 et 3168 sont des nombres importants à Stonehenge, 19008 étant 11 x 12³. Ce périmètre pourrait également être interprété, comme le fait Dennis, comme 504 mètres de 39,375", 504 étant 12 x 6 x 7.

Dans l'image ci-dessous, Dennis présente plus de mesures de Teotihuacan. Ce qui est intéressant ici, c'est que le nombre total de pieds qu'il arrive pourrait être interprété comme proche de 1900,8 x 29,53059 / 12 = 4 677,64, bien qu'il soit un peu plus long d'un pied que 4 676,53.

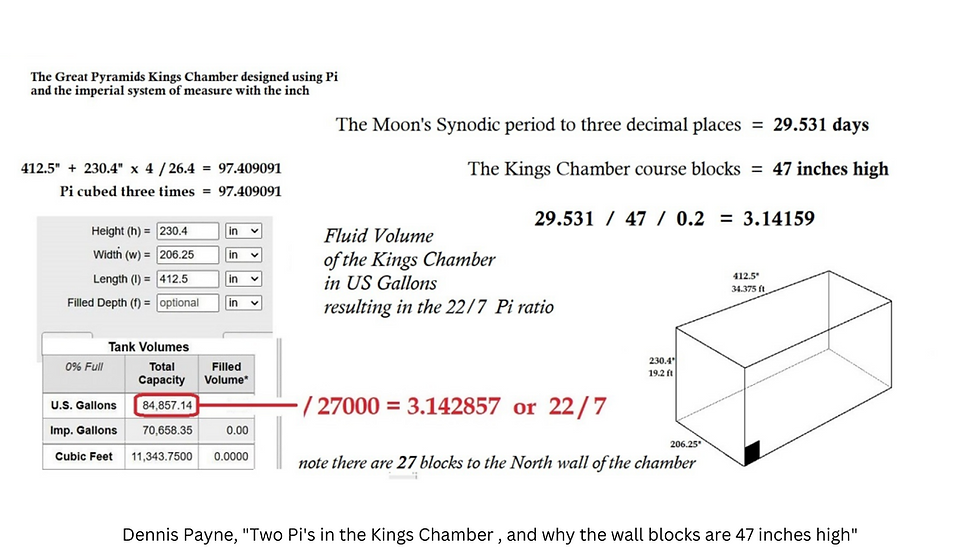
Dans l'image suivante, Dennis montre que le nombre 47 et la période des Lunes de 29,531 jours, codant Pi, peuvent être vus dans les dimensions des plates-formes de la Citadelle. Denis écrit :

Si nous acceptons l'idée que ces plates-formes ont été conçues de manière à coder certains ensembles d'informations, alors il serait important d'obtenir une détermination précise de la façon dont elles se rapportent les unes aux autres via leurs distances mesurées , dans ce cas, je Je fais référence à la distance entre chacune des quatre plates-formes inférieures et la plate-forme centrale de la Plaza, et encore une fois, j'utilise le système de mesure impérial pour découvrir ce qui peut être caché. Comme vous pouvez le voir sur la capture d'écran, j'ai mesuré les quatre distances entre les plates-formes inférieures et celle centrale. Les quatre combinés = 1566,67 pieds et x 3 = 4700 pieds. Puis le cycle des Lunes de 29,531 / 4700 / 2 = 3,141596. Le nombre 47 a également été trouvé dans la chambre des rois des grandes pyramides, en ce sens que chaque cours mesure 47 pouces de haut.

Le nombre 47

Dennis a découvert une connexion lunaire au nombre 47, comme le montre le premier schéma de son posté ici, et Jim Wakefield a également trouvé ce nombre en relation avec un site antique et la lune.

Jim Wakefield a découvert un fait métrologique curieux au cercle de pierres de Rollrights: que le nombre 47 est un nombre lunaire. Comme nous l'avons vu, il y a 29,53059 jours dans un mois lunaire moyen, et 12 à 13 mois lunaires par an, et il y a des cycles de mois lunaires qui coïncident avec des cycles d'années solaires, comme le cycle Métonique de 19 ans, ou 235 mois lunaires. Le nombre 47 est simplement 235 x 2 / 10. Ce que Jim a découvert, c'est qu'un cercle avec un rayon de 47 unités aura une circonférence de presque exactement 10 mois lunaires exprimés dans la même unité. Autrement dit, 47 x 2 x pi = 29,53097 x 10.

Encore plus remarquable est l'autre aspect lunaire d'un cercle avec un rayon de 47 unités, que Jim a trouvé : que la surface d'un tel cercle aura presque exactement le même nombre d'unités qu'il y a de jours dans un cycle de Métonique.

Cycle métonique : 29,53059 x 235 = 6939,68865

aire du cercle de rayon 47 unités : 47² x pi = 6939,77817 unités au carré

L'unité dans laquelle cela était exprimé aux Rollrights était le pied nord ou saxon de 13,2 pouces ou 0.33528 metres. Jim écrit à propos de :

la coïncidence du cercle Rollright ayant un diamètre de 94 pieds saxons et donc une circonférence de '295,309 pieds saxons équivalant au nombre de jours dans un mois synodique 29,53059 jours, puis la superficie du cercle ayant 6939,778 pieds saxons carrés équivalant au nombre de jours dans un cycle métonique 6939,75 jours (1)

Le pied saxon est une unité ancienne, généralement considérée comme 13,2 pouces, avec des liens directs avec l'Inde, car 13,2 pouces correspondent à 200 angles de 0,066 pouces. En 1930-31, à Mohenjo-daro, Ernest Mackay découvre un morceau d'obus brisé portant 8 divisions de 6,7056 mm chacune, ce qui équivaut à 0,264 pouces. Un pied saxon mesure 50 x 0,264 pouces. 96 Angulas font un Dhanusha ordinaire, et cela représente exactement un millième de mile anglais. Les liens entre les systèmes de mesure anglais et indien remontent loin dans le temps.

Il est d'autant plus curieux que le nombre 47 fonctionne si bien au sein d'un cercle pour décrire dix mois et un cycle métonique par la circonférence et l'aire, alors que le nombre de mois dans 2 cycles métoniques est de 470. Sans invoquer de cercles, le nombre 47 relie les cycles solaire et lunaire : 38 années de 365,242199 jours sont presque exactement égales à 470 lunaisons de 29,53059 jours. De plus, 38 x 2/47 fournit une bonne approximation de la relation presque Phi entre les cycles du soleil et de la lune, puisque 76/47 = 1,61702127 et 29,53059 x 20/365,242199 = 1,6170415. Le nombre moyen de lunaisons par année solaire peut être considéré comme étant de 47 x 20 / 76. Une année en jours est très proche de 29,53059 x 20 x 47 / 76. Le mètre en tant que mesure en pouces se rapporte aux cycles du soleil et lune, avec 39,3700787402 x pi/10 est égal au nombre moyen de lunaisons dans une année. Le mètre en pouces multiplié par 76 x pi / 200 est presque égal à 47.

Comme illustré précédemment, Dennis Payne a également découvert le lien entre les cycles lunaires et le nombre 47 à Gizeh : à l'intérieur de la Chambre du Roi, dans la Grande Pyramide, la hauteur des blocs de parcours est de 47 pouces.

Piazzi Smith et Petrie conviennent tous les deux que les hauteurs de cours de la chambre des Rois sont de 47 pouces de haut, avec un minuscule + - de 0,040. On doit se demander pourquoi ces blocs ont été fabriqués à cette hauteur, si l'on croit qu'ils n'ont utilisé que des coudées pour leurs mesures alors le tailleur de pierre ferait-il s'il lui était demandé de faire ces blocs de 2,279340446 coudées de haut, en supposant qu'il ait utilisé cette coudée bien connue de 20,62 pouces [0.523748 m]. (2)

Le nombre 47 est-il un élément important de la métrologie historique plus généralement ? Peut-être que ce lien entre la circonférence et l'aire d'un cercle, exprimé par pi et le nombre 47, a une application plus large ?

Irv Bromberg a un autre lien entre le nombre 47 et la lune. Il écrit:

Il y a 235 mois par cycle de 19 ans du calendrier hébreu. Les diviseurs de 235 sont 1, 5, 47 et 235, alors que 19 est un nombre premier. Le nombre moyen de mois par année civile hébraïque traditionnelle = 235/19, donc le nombre d'années dans le cycle de répétition du moment molad = 25920 / (235/19) = 2095+31/47 ans. Tous les 18 mois, le moment molad est exact à la minute avec zéro pièce restante. Tous les 1080 mois ou 87 + 7/22 ans, le moment molad est exact à l'heure avec zéro minute et zéro partie restante, ce qui s'est produit le plus récemment pour le moment molad traditionnel de Cheshvan en l'an 5765. Un cycle complet de chaque atterrissage possible du moment molad chaque jour de semaine possible prend 7 × 25 920 = 181 440 mois / (235/19) = 689 472 / 47 = 14 669 + 31/47 ans (il faut s'y attendre car 181 440 est le nombre de pièces par semaine). Un cycle complet pour le molad de Tishrei de la première année du cycle de 19 ans pour passer par chaque moment de molad possible atterrissant chaque jour de semaine possible prend 47 fois plus de temps, soit 689472 ans. (3)

Irv Bromberg a fait remarquer :

Il y a 235 mois par cycle de 19 ans du calendrier hébreu. Les diviseurs de 235 sont 1, 5, 47 et 235.

Il explique ce qu'est l'intervalle molad dans le calendrier hébreu, et termine en disant :

Un cycle complet pour que le molad de Tishrei de la première année du cycle de 19 ans passe par chaque moment de molad possible atterrissant chaque jour de semaine possible prend 47 fois plus de temps, soit 689 472 ans.

Pour toutes les raisons ci-dessus, il est clair que 47 est un nombre lunaire important. Il existe un autre cycle associé au nombre 47 et il est connecté à Mars. Cette planete revient à la même position par rapport à la terre et au soleil après 47 ans, soit 22 x 780 jours. Ce cycle était connu dans l’ancienne Mésapotamie.

47 est aussi le numéro atomique de l’argent, un métal associé à la lune.

Dennis Payne a découvert que le nombre 47 relie également la vitesse de la lumière au rayon équatorial de la Terre. Ainsi, le nombre de fois que la lumière pourrait, si elle le pouvait, traverser le centre de la Terre depuis l'équateur en une seconde est de 47,003139 (en utilisant 186 282,39 mps et 3963,1906 miles), et 47 x π x 2/10 - 29,53097, et 47 x 47 x π = 6939,778, nombre de jours dans un cycle Metonic, et 47 x 10/2 = 235, le nombre de mois lunaires dans le cycle Metonic, plus il y a le lien entre 47 et le calcul du molad.

Angle de précession, MeMoRY, Wikimedia Commons

On pourrait aussi définir la vitesse de la lumière comme :

29,53125 x 400 000 000 x 1224/1225 pouces par seconde, en utilisant 29,53125 comme longueur en jours d'une lunaison. Même avec la bonne moyenne de lunaison, 29,53059, vous obtenez toujours 299 785 871,3022 mètres par seconde, toujours proche des 299 792 458 mps officiels.

Curieusement, la Lune s'éloigne progressivement de la Terre, vers une orbite plus élevée, et théoriquement dans environ 50 milliards d'années, la Terre et la Lune seront en rotation synchrone, et l'orbite de la Lune aura changé de 27 à 47 jours.

L’angle de précession du cycle des équinoxes mesuré à partir du centre de la terre a été évalué à 47 degrés.

Stephen Dail a utilisé le nombre 47 pour exprimer les valeurs de diamètre lunaire. 47 est 22 + 25, et ces deux nombres sont les numérateurs de deux approximations Pi, 22/7 et 25/8, impliquées dans tant de ses calculs, ainsi que son chiffre pour l'ApoTerrien de 25 unités, et le Périterririen de 22 unités du cycle orbital excentrique de la Lune. La valeur 47 / 2 = 23,5 devient le demi-grand axe de la distance moyenne de la Lune à la Terre dans son cycle orbital mensuel, étant également la distance canonique mentionnée par John Michell.

Une année peut être définie à l’aide du nombre 47, comme 153/(47 x 28) x 1000 x pi = 365,245954. Le 153 se retrouve dans l'histoire biblique du poisson dans le filet, et le 28 est lunaire dans le sens où il dure 4 semaines de 7 jours. Ainsi, un cercle d'un diamètre de 153 x 1000 /(47 x 28) aurait une circonférence de 365,245954. Si l'on remplace le nombre 1000 dans cette somme par le nombre de jours de repos dans un lunation, cela nous donne approximativement la différence en jours entre une année solaire et lunaire : 153 / (47 x 28) x 29,53059 = 10,785929 et 365,242199 - 354,36708 = 10,875119. . Il est également intéressant de noter que 153 x 10 000 / (28 x 47) pouces correspondent à 29,530395 mètres. Nous pourrions même considérer le mètre comme 153 x 10 000 / (28 x 47 x 29,53059) = 39,3698189 pouces. On peut même considérer le cycle métonique comme 153 x 100 000 / 56 pouces convertis en mètres : 6939,64286 jours.

Il existe également un lien intéressant avec le yard mégalithique, dans le cadre d'une vesica piscis, comme ci-dessous.

À Gizeh, Flinders Petrie a donné la longueur de la distance entre les centres de la Grande Pyramide et la troisième pyramide à 36 857,7 pouces, soit 936,18558 m. Si cette ligne est la diagonale d'un rectangle, la longueur, nord-sud, est de 29 102 pouces, ou 739,1908 m, et la largeur, ouest-est, est de 22 616 pouces, ou 574,4464 m. Si nous prenons la largeur et la multiplions par 29,53059, le nombre de jours d'une lunaison, et par 38, nous obtenons la longueur. Et inversement, si l’on multiplie la longueur par 365,242199, le nombre de jours dans une année, et que l’on divise par 470, on obtient à nouveau la largeur. C'est un rectangle métonique.

22616 x 38 / 29,53059 = 29102

29102 x 365,242 / 470 = 22616

Le nombre 47, combiné au nombre 38, est présent dans ce rectangle de Gizeh, qui s'étend entre les centres de la Grande et de la troisième pyramide de Gizeh. Une lunaison de 29,53059 jours, multipliée par 47 x 10 et divisée par 19 et 2, donne approximativement l'année solaire 365,24677. Cela signifie que le nombre de mois lunaires en moyenne par an peut être simplifié à 470/38, soit 12,36842 et 365,242199 / 29,53059 = 12,368266. Ce rapport solaire et lunaire est légèrement différent de celui trouvé aux Rollrights par Jim Wakefield, mais il utilise également le nombre 47. Aux Rollrights, le rayon d'un cercle était de 47 pieds saxons et la circonférence était d'environ 10 mois lunaires en jours exprimés en pieds saxons. À Gizeh, nous avons un rectangle, et le rapport entre la largeur et la longueur est de 38/29,53059, à environ un demi-pouce près : ce qui est à peu près égal à 365,242199/470. La largeur de 22616 x 38/29,53059 = 29 102,29697. La longueur donnée par Flinders Petrie est 29102. Ce 29102 multiplié par 365,242199 / 470 = 22 615,47379, soit 0,5262 pouces de moins que le chiffre de Flinders Petrie.

Un système de mesure basé sur la lune ?

Nous pouvons écrire une lunaison en jours comme approximativement 47/5 π, ou 94π, et donc étroitement associée à la géométrie du cercle. Et si le mètre était compris comme une expression du mois lunaire en pouces, multiplié par un facteur. Peut-être pourrions-nous penser au mètre comme 29,53059 x 4/3 pouces, ou simplement 47 x 4/15 x π pouces ? Cela donnerait une valeur pour le mètre de 39,374628 pouces, ce qui n'est pas loin de 39,375", une valeur historique, ou de la valeur actuelle de 39,3700787402".

Peut-être pouvons-nous aussi penser au shusi, la cour mégalithique et au pied nord ou saxon, que Jim Wakefield a trouvé aux Rollrights, comme exprimant les nombres lunaires en pouces, multipliés par un simple facteur.

Le mètre, exprimé en pouces, est proche du rapport entre l'année solaire et le mois lunaire, x 10/π. Le lien entre le mètre et le pouce pourrait peut-être aussi être compris en termes de soleil et de lune. 1000 x pi lunaisons correspondent à près de 254 ans et 1 mètre correspond à 1/254 pouces.

Le rôle de l'astronomie dans l'histoire de la mesure est contesté. Il n'y a pas grand-chose dans la littérature pour attester que l'astronomie est utilisée comme base pour les systèmes de mesure, c'est pourquoi les découvertes à Gizeh et dans les cercles mégalithiques sont si intrigantes. Il semble que lorsque vous regardez directement les pierres et leurs mesures, il pourrait bien y avoir des signes que le cycle de la lune et sa relation avec le soleil sont en fait au cœur des anciens systèmes métrologiques.

Cette connexion peut également être trouvée dans les systèmes de mesure modernes, bien qu'elle soit là par conception ou par coïncidence est une question ouverte. Par exemple, il existe un lien entre le mile et les cycles du soleil et de la lune.

Vous trouverez ci-dessous des images pour illustrer ces connexions.

Si, à Gizeh, la même mesure linéaire peut produire 80 années solaires en pouces ou 4 années lunaires en coudées (le côté ouest-est du rectangle), qu'est-ce que cela nous apprend sur la relation entre les pouces et les coudées ? Le rapport entre 80 années solaires et 12 années lunaires est de 20,613777. Divisé par pi et 10, cela nous donne 0,656157, qui pourrait être une mesure ou le shusi en pouces, qui ensuite multiplié par 10/9 donne 0,7290362, qui pourrait être une mesure du chiffre égyptien en pouces. Une coudée de 20,61377 pouces est également très proche de pi/6 mètres. Vous obtiendriez un mètre de 39,36941 pouces 20,613777 x 6/pi = 39,3694141

864

864 est également exactement un trentième du chiffre traditionnel donné à la longueur d'un cycle de précession en années, 25 920. Les années solaires et lunaires, et l'oscillation de la rotation de la terre sur son propre axe, sont toutes liées au nombre 864. La relation entre les années solaires et lunaires peut être exprimée comme pi multiplié par la longueur d'un cycle précessionnel ou Grande Année (valeur traditionnelle) divisé par 30 000. Si mille mois lunaires de 29,53059 jours et le nombre de jours de différence entre les années solaires et lunaires, 10,875119, puis divisé par pi en 22/7, donne 864, alors 3 000 mois lunaires donnent, de la même manière, le cycle de précession. 30 000 x 29,53059/10,875119 x (7/22) = 25 919,983, appelez-le 25 920. Michael S. Schneider souligne que 86 400 000 est un très beau chiffre. Il demande:

Combien y a-t-il de millisecondes dans une journée ?

Évidemment, 1000 millisecondes/seconde x 60 secondes/minute x 60 minutes/heure x 24 heures/jour = 86 400 000

ou, plus proprement = 55 x 44 x 33 x 22 x 11

La différence moyenne en jours entre l'année lunaire et l'année solaire, 10,87512 jours, en termes de pi, ou au moins, une approximation de pi : une façon d'exprimer la différence moyenne entre l'année lunaire et l'année solaire est avec 19/7, ou plus précisément, 19.008/7, qui peut aussi s'exprimer par 864 x 22/7 000, ce qui est proche de 864 x Pi. On pense que la fraction 22/7 a été une approximation couramment utilisée de Pi dans l'Antiquité, utile pour préserver des nombres entiers dans les mesures de diamètres et de circonférences d'un même cercle, et une sorte de solution pragmatique au problème de l'incommensurabilité entre le diamètre et la circonférence qui 'vrai' pi présente. Son utilisation a été déduite d'études de dispositions circulaires dans des monuments de l'Antiquité. Le nombre de jours d'un mois lunaire divisé par la différence de jours entre douze mois lunaires et une année est donc très proche de Pi puisque 22/7 fois 0,864. Douze mois lunaires de 29,53059 jours donnent une année lunaire de 354,36708 jours. C'est 10,875119 jours de moins qu'une année solaire de 365,242199 jours. Vous pourriez dire que pi lui-même peut être approximé comme 1 lunaison / différence de jours entre douze mois lunaires et une année divisée par 0,864.

29.53059 / 10.875119= 2.7154268

864 x 22 / 7 000 = 2,71542857

Le nombre 864 peut être associé aux années lunaires et solaires. Un cercle d'un diamètre de 864 unités aurait une circonférence d'environ 1 000 lunaisons / la différence de jours entre les années solaires et lunaires. Par coïncidence, le soleil a un diamètre de 864 000 milles. On pourrait donc dire que le soleil a, en miles, une circonférence de 1 000 000 de lunaisons / la différence de jours entre les années solaires et lunaires.

Lunatique

Si rien d'autre, ces découvertes lunaires sont intrigantes. Les nombres lunaires ont-ils été délibérément inscrits dans la Grande Pyramide et les cercles mégalithiques ? Si tel est le cas, ils font preuve d'une sophistication et d'une complexité incroyables. Le mouvement de la lune est potentiellement un moyen de suivre le temps, mais aussi de mesurer l'espace.