88. Alignement Mégalithique de Plouharnel de Quentin Leplat : Géométrie, Mesures et Implications Astronomiques

Les mégalithes antiques de Bretagne fascinent depuis longtemps chercheurs et passionnés. Parmi ceux qui ont approfondi leurs mystères figure Quentin Leplat, dont le documentaire « Arpenteurs du Néolithique », disponible sur YouTube , propose une exploration approfondie de ces structures énigmatiques. L'ouvrage de Quentin Leplat, également publié dans un article sur Academia, et complété par des vidéos de suivi (voir ici (pour le premier), apporte des preuves convaincantes que ces sites mégalithiques n'étaient pas des monuments isolés, mais faisaient partie d'un vaste réseau interconnecté, façonné par des connaissances avancées en géométrie et en astronomie. Ses recherches révèlent une compréhension approfondie de l'espace et de l'alignement, incitant à réévaluer la façon dont les hommes préhistoriques percevaient et interagissaient avec leur environnement.

L'un des aspects les plus fascinants de cette recherche réside dans la précision géométrique qui sous-tend ces constructions anciennes. Des chercheurs comme Howard Crowhurst ont apporté une contribution significative à ce domaine, démontrant comment les bâtisseurs mégalithiques utilisaient des principes mathématiques complexes, notamment l'utilisation de carrés, de doubles carrés, de triples carrés, etc., pour former des rectangles qui constituaient la base de la géométrie du sol. Cette approche géométrique suggère que le positionnement des dolmens, menhirs et autres structures n'était pas arbitraire, mais obéissait à une logique spatiale délibérée, liée à la géométrie et aux cycles astronomiques.

Lors de son étude des dolmens de la commune de Plouharnel, dans le Morbihan, Quentin Leplat a identifié un alignement de quatre dolmens s'étendant sur 7 817 mètres. Bien que la région compte de nombreux dolmens répertoriés, le hasard statistique ne suffit pas à expliquer l'extraordinaire précision de cet alignement. Mesurés à la fois avec Google Earth et un GPS de haute précision, les dolmens suivent une ligne droite avec une déviation angulaire de seulement ±0,07°, correspondant à un étroit couloir de seulement 4 mètres de large.

Au-delà de la précision de leur positionnement, l'espacement des dolmens suggère un principe géométrique sous-jacent. Les distances qui les séparent suivent une séquence proportionnelle basée sur la racine carrée de 10 (√10). Cette relation, associée aux anciennes unités de mesure et aux cycles célestes, témoigne d'une compréhension avancée des mathématiques, de la géométrie et de l'astronomie chez les bâtisseurs du Néolithique. Cet article vise à présenter le travail de Quentin Leplat sur cet alignement, à en analyser la géométrie et les dimensions, et à réfléchir à l'intention des géomètres.

La géométrie de l'alignement

Comprendre les mégalithes de cette région exige de dépasser la perspective d'un site isolé et de les considérer comme des nœuds d'un vaste réseau spatial et culturel. Les dolmens et autres structures semblent être précisément implantés dans le terrain. Leur répartition suggère que les bâtisseurs du Néolithique possédaient une connaissance approfondie de l'astronomie, leur permettant de suivre d'importants cycles solaires et lunaires. Nombre de ces sites coïncident avec des solstices, des équinoxes et des arrêts lunaires importants, ce qui renforce l'idée que leur emplacement était loin d'être fortuit. L'analyse de ces structures sous l'angle de la géométrie et de l'astronomie permet de commencer à déchiffrer leur fonction. Les dolmens et menhirs de Bretagne n'étaient probablement pas de simples lieux funéraires ou marqueurs territoriaux, mais faisaient partie d'un système bien plus vaste de transmission du savoir, fonctionnant comme des points de référence dans un paysage conçu pour encoder les mouvements célestes, au sein d'un ancien système d'observation reliant les rythmes terrestres et cosmiques. Cette réinterprétation des mégalithes bretons remet en question les hypothèses archéologiques conventionnelles et ouvre la voie à une compréhension plus approfondie des sciences, de la spiritualité et de la société préhistoriques. En étudiant ces sites dans leur ensemble, plutôt que de manière isolée, nous pouvons acquérir de précieuses connaissances sur les réalisations intellectuelles et culturelles du monde néolithique.

Structure de la ligne

L'alignement est composé de quatre dolmens :

• Kergazec

• Mané er Mor

• Runesto

• Mané-Roularde

  
  

Quentin Leplat a concentré son analyse sur ces quatre dolmens en raison de leurs distances respectives le long de l'alignement. Le premier segment de l'alignement, de Kergazec à Mané er Mor, représente précisément 1/10e de la longueur totale (718,7 mètres sur 7 817 mètres). Le second segment, de Kergazec à Runesto, mesure 2 472 mètres, démontrant la présence du facteur √10 (racine carrée de dix).

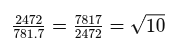
Cette relation mathématique n'est pas arbitraire. La diagonale d'un triple carré (un rectangle composé de trois carrés côte à côte) est précisément √10 fois la longueur du côté d'un carré. Cela suggère que les constructeurs utilisaient une conception modulaire sophistiquée basée sur des principes géométriques. De plus, en analysant l'azimut de l'alignement, Quentin Leplat a appliqué son expertise en géométrie ancienne et a constaté que son angle (21,825°) correspond étroitement à la diagonale d'un rectangle de 2 x 5 carrés (21,801°), renforçant la théorie d'une utilisation délibérée d'un plan géométrique structuré. Ces rapports sont précis et prouvent que les constructeurs de ces dolmens avaient une connaissance sophistiquée de la géométrie.

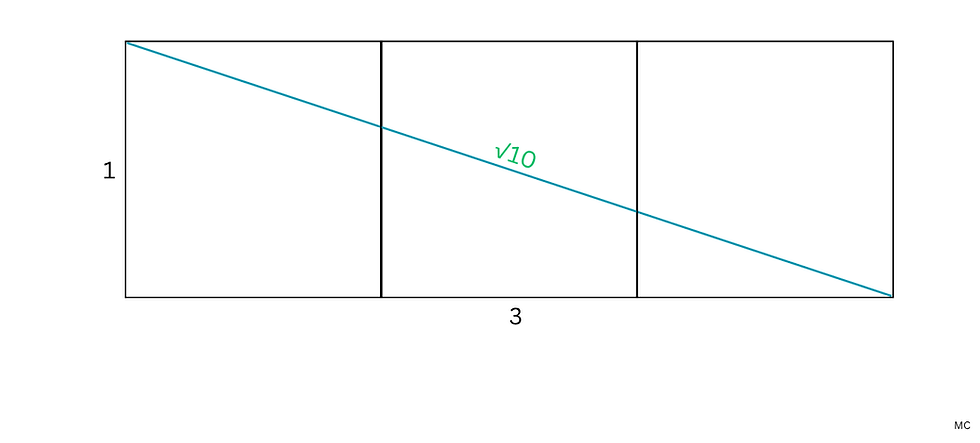
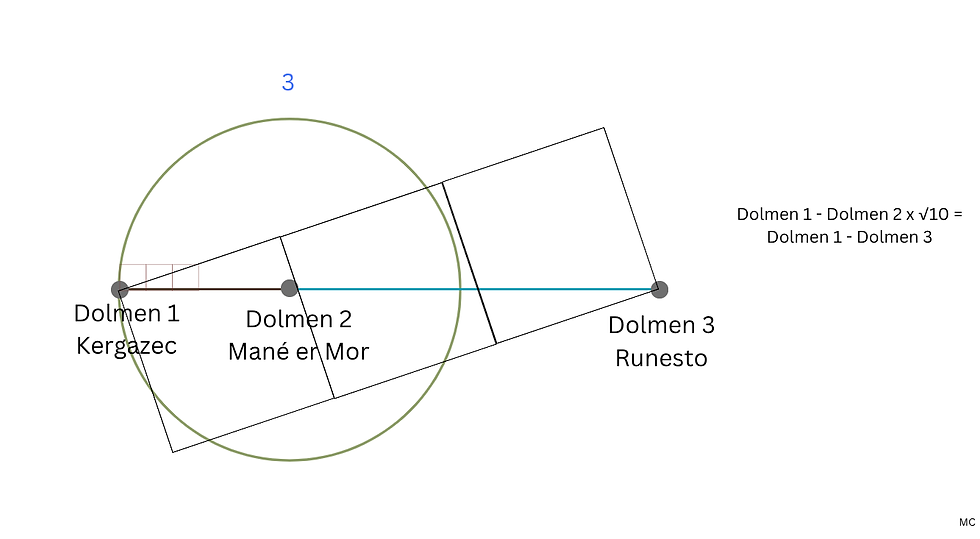
Je voulais visualiser le lien entre la multiplication d'un segment par la racine carrée de dix et le fait que cette racine soit, géométriquement, la diagonale d'un rectangle de 1 x 5. J'ai donc expérimenté quelques constructions et découvert que le premier segment de l'alignement, entre les deux premiers dolmens, peut être considéré comme le diamètre d'un cercle. Ensuite, un carré est inscrit, de sorte que trois de ses coins touchent le centre et la circonférence du cercle. Le carré est orienté par rapport à un triple carré, pour obtenir l'angle droit, et décalé de sorte qu'un seul coin touche la circonférence. Le carré est ensuite prolongé en un rectangle de 3 x 1 (trois carrés côte à côte), et la diagonale est tracée. Cette diagonale correspond alors au deuxième segment de l'alignement, entre les dolmens 2 et 3. Le même processus est ensuite répété pour obtenir le troisième segment et la position du dolmen 4.

Considérations paysagères : visibilité et élévation

En regardant le film de Quentin Leplat, il m'a semblé que l'une des caractéristiques les plus frappantes de cet alignement était que les quatre dolmens sont situés à des points élevés du paysage. Ce positionnement assure leur visibilité à grande distance, renforçant l'idée qu'il s'agissait de marqueurs délibérés plutôt que de structures disposées au hasard. Ce placement stratégique suggère une méthode de relevé avancée. Ces dolmens étaient donc très probablement des marqueurs visuels.

Que nous apprennent les dimensions ?

Connexions avec les systèmes de mesure anciens

Les distances mesurées correspondent étroitement au yard mégalithique (YM), identifié par le professeur Alexander Thom sur des sites mégalithiques à travers l'Europe. L'alignement correspond à la diagonale d'un rectangle composé de deux carrés sur cinq, chaque carré ayant un côté mesurant 1 451,6 mètres. Cela peut être interprété comme 7 000 / 4 yards mégalithiques. De plus, la longueur totale de l'alignement, soit 7 817 mètres, établit un lien entre le yard mégalithique et le nombre π. Cette distance correspond à la circonférence d'un cercle de 3 000 yards mégalithiques de diamètre, comme l'a montré Quentin Leplat.

Le mois draconitique exprimé en jours, multiplié par 6/5 et interprété comme une valeur en pouces, donne 32,65464, une valeur acceptable comme yard mégalithique. Et comme l'a observé Quentin Leplat, le premier segment correspond à la circonférence d'un cercle de 300 YM de diamètre. Une autre façon d'envisager cela est de prendre une ligne de 365,242199 x 4 x 12^3 / (29,53059 x 1000) pouces et de la diviser par 2,61803, Phi au carré. Cela donne un résultat de 32,654116 pouces, soit un yard mégalithique en pouces (2,721176 pieds). Cela fonctionne grâce à la relation approximative de 5/6 entre pi et phi au carré.

Les pouces, les mètres et d'autres unités peuvent également être utilisés pour interpréter les dimensions de cette ligne. Une relation mathématique convaincante émerge de la comparaison de trois cycles astronomiques : le mois draconitique (27,2122 jours), la lunaison ou mois synodique (29,53059) et l'année solaire tropicale (365,242199 jours) : le nombre moyen de lunaisons par an (365,242199 / 29,53059) est très proche du mois draconitique exprimé en jours multiplié par 1 000 π / (12³ x 4).

27,2122 x 1000 π / (12³ x 4) ≈ 365,242199 / 29,53059

Ce n'est pas tout à fait exact, car 27,2122 x 1000 π / (12³ x 4) x 29,53059 = 365,24302, mais la correspondance est très proche, à 99,999775 %.

Si nous considérons ces valeurs comme des mesures en pouces et que nous examinons les différentes parties de cette équation, nous pouvons obtenir une approximation très précise d'autres unités de mesure importantes.

27,2122 x 10 000 / (12³ x 4) = 39,369502, très proche d'un mètre.

365,242199 / (29,53059 π) x 10 = 39,369414, très proche d'un mètre.

On peut relier cela à une autre équation astronomique et géométrique, impliquant le mois sidéral de 27,321661 jours ainsi qu'une lunaison, et 235, le nombre de lunaisons d'un cycle métonique : 10 000 / (235 x 29,53059 / 27,32166) = 39,370154. C'est également très proche d'un mètre en pouces.

On pourrait donc interpréter le premier segment de l'alignement comme suit :

• 12⁵ π / 1000 = 781,7287 mètres (une valeur peut-être un peu élevée, et donc à écarter comme interprétation possible)

• 12⁵ / 100 x 365,242199 / 29,53059 = 30 776,2042 pouces (781,7156 m)

• 360 π x 27,2122 = 30 776,2731 pouces (781,7174 m)

  
  

Ces deux dernières options offrent deux façons d'interpréter les dimensions de l'alignement par rapport à l'astronomie et au pouce, avec un haut degré de précision, un pouce représentant un jour. Ailleurs, notamment en Bretagne et en Égypte, le pouce a été identifié comme une unité correspondant à un jour (1). Lus comme des mesures en pouces, le mètre et le yard mégalithique peuvent être compris comme des mesures astronomiques. Un mètre par exemple peut être approximativement vu comme le nombre moyen de lunaisons par an, multiplié par 10 et divisé par π, comme une mesure en pouces. Un yard mégalithique peut être compris comme le nombre moyen de lunaisons par an divisé par π également, mais ensuite multiplié par 12⁴ x 4 / 10 000. Le yard mégalithique peut également être compris comme un mois draconitique en jours multiplié par 6 / 5, toujours comme une mesure en pouces. Grâce à ces liens, il est intéressant de noter que le premier segment de l'alignement, et sa longueur totale, dix fois supérieure à celle du premier segment, peuvent être interprétés en relation avec le nombre moyen de lunaisons par an (365,242 199 / 29,53059), ou le mois draconitique en jours et π. L'interprétation de ces unités de mesure semble obéir à la même logique que celle des longueurs de l'alignement.

L'étude de Quentin Leplat explore les relations géométriques présentes dans les structures mégalithiques, démontrant que leur disposition reflète une connaissance approfondie de la métrologie et des cycles astronomiques. Plus précisément, le yard mégalithique pourrait avoir été dérivée des périodicités lunaires et solaires, reliant la conception architecturale aux observations célestes. En résumant ces idées fondamentales dès le départ, les lecteurs pourront mieux contextualiser les discussions techniques ultérieures et apprécier les implications plus larges de cette recherche.

Considérations métrologiques : le pouce comme unité de temps

Quel pourrait être le but de cet alignement, long de près de huit kilomètres ? Une possibilité convaincante est qu'il encode les cycles nodaux lunaires. L'orbite de la Lune croise l'écliptique en deux points (nœuds), qui régressent sur un cycle de 18,6 ans. Le mois draconitique, qui mesure le temps entre deux croisements successifs du même nœud, est de 27,2122 jours. Nous avons vu que ce cycle peut être lié à une mesure linéaire : 360 x 27,2122 π = 30 776,27, et, en pouces, cela correspond exactement à 781,7173 mètres, soit la longueur entre les deux premiers dolmens (781,7 m) et un dixième de l'alignement total. Le premier segment multiplié par √10 donne 2 472,007 mètres, soit la distance entre le premier et le troisième dolmen (2 472 m), et multiplié par 10, la distance totale (7 817 m).

1. Interprétation par le mois synodique

La longueur de l'alignement, 7 817 mètres, représente un dixième de l'ensemble et peut également être interprétée comme 12⁵ / 100 x 365,242199 / 29,53059 = 30 776,2042 pouces, un pouce représentant un jour. Il s'agit du nombre moyen de mois lunaires dans une année (365,242199 / 29,53059) exprimé en pouces, multiplié par 12 à la puissance 5 et divisé par 100. Le système impérial est également en partie duodécimal, il y a donc un lien intéressant ici.

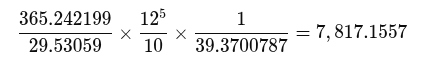
2. Interprétation par le mois draconitique

   
   

   Si le premier segment peut être interprété comme 360 ​​π x 27,2122 = 30 776,2731 pouces, 360 représente les degrés d'un cercle complet, π se rapporte au mouvement circulaire et 27,2122 au mois draconitique en jours. (30 776,2731 pouces correspondent à 781,71734 mètres))

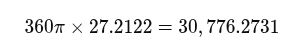
Une possibilité convaincante est que cet alignement encode les cycles nodaux lunaires, essentiels à la prédiction des éclipses. L'orbite de la Lune est inclinée par rapport à celle de la Terre autour du Soleil, et sa trajectoire croise l'écliptique en deux points, appelés nœuds. Ces nœuds régressent sur un cycle de 18,6 ans, ce qui signifie que, durant cette période, ils effectuent un tour complet en sens inverse le long de l'écliptique. La compréhension de ce cycle est essentielle pour prédire les éclipses, qui ne se produisent que lorsque le Soleil est proche d'un nœud lunaire lors d'une pleine ou d'une nouvelle lune.

Un mois draconitique correspond à la durée entre deux passages successifs de la Lune par le même nœud, soit précisément 27,2122 jours. Les constructeurs de ces monuments ont peut-être utilisé des mesures linéaires spécifiques pour coder les connaissances astronomiques.

La présence de 360 ​​× π × 27,2122 dans le premier segment (et multipliée par 10 dans l'alignement complet) suggère qu'il pourrait s'agir d'un phénomène circulaire, périodique et lié au mouvement de la Lune. La question se pose alors : quels cycles ou mesures cette équation pourrait-elle représenter ? Plusieurs possibilités existent quant à son lien avec les cycles lunaires et l'observation astronomique. Chacun des cycles suivants joue un rôle dans le mouvement lunaire :

1. Précession des nœuds lunaires (cycle de 18,6 ans). Les nœuds lunaires (les points où l'orbite de la Lune croise l'écliptique) se déplacent progressivement vers l'arrière dans le zodiaque sur 18,6 ans sous l'effet des interactions gravitationnelles. Ce cycle détermine quand et où les éclipses peuvent se produire sur de longues échelles de temps. Une représentation physique de ce phénomène pourrait consister à marquer les mois draconiques à intervalles réguliers le long d'une ligne, montrant ainsi le décalage des nœuds au fil du temps.

2. Distance de la Lune à la Terre. L'orbite de la Lune est elliptique, ce qui signifie que sa distance à la Terre varie cycliquement. Cette variation suit le mois anomaliste (~27,55 jours), proche du mois draconitique. Cet alignement pourrait-il représenter les variations de la distance lunaire au fil du temps ? Ce serait une autre façon de relier le mouvement angulaire (360°) à une oscillation périodique.

3. Lien avec le mois sidéral (27,3217 jours). Le mois sidéral est le temps que met la Lune pour revenir à la même position par rapport aux étoiles. Les différences entre le mois draconitique (27,2122 jours) et le mois sidéral (27,3217 jours) s'accumulent au fil du temps, influençant les cycles d'éclipses. Un alignement physique pourrait suivre ces changements progressifs en marquant les intervalles des mois draconitiques tout en montrant comment ils divergent des cycles sidéraux.

4. Mouvement angulaire et 360° comme unité de conversion espace-temps. La Lune effectue un tour complet de 360° sur son orbite environ tous les 27,3 jours (mois sidéral). Si l'on multiplie un mois draconitique (27,2122 jours) par 360, on obtient une mesure angulaire du temps : 360 × 27,2122 = 9 796,4360. Ce nombre pourrait être converti en distance linéaire, représentant la distance parcourue par la Lune sur son orbite au cours de cette période. Cela suggère un système où le temps est converti en unités spatiales, possiblement avec π comme facteur de conversion.

5. Rapports avec d'autres cycles (cycles métonique et saros). Le cycle métonique (19 ans, environ 235 mois lunaires) aligne les calendriers solaire et lunaire. Le cycle de Saros (18 ans, 11 jours, environ 223 mois lunaires) est le cycle répétitif des éclipses. Le mois draconitique joue un rôle dans les deux cycles, en particulier celui de Saros, où les éclipses se produisent à peu près au même endroit dans le ciel après 18 ans et 11 jours. L'équation pourrait coder un moyen de suivre ces retours d'éclipses périodiques en marquant les mois draconiques selon un motif linéaire ou géométrique.

6. Longitude et latitude de la lune. L'orbite elliptique provoque des variations de vitesse en longitude (~12°-15° par jour) et une étude de la position de la lune montrerait ces variations. La compréhension de ce mouvement est essentielle pour la prédiction des éclipses, car le retour de la Lune à un nœud détermine le moment où une éclipse pourrait se produire.

   
   

Le graphique ci-dessous montre la longitude lunaire en fonction du temps sur un mois draconique (27,2122 jours). Le mouvement est essentiellement linéaire, représentant le mouvement moyen de la Lune d'environ 13,23° par jour, avec toutefois une légère variation sinusoïdale due à son orbite elliptique.

Le graphique ci-dessous montre également la longitude de la Lune sur un mois draconitique, mais avec un deuxième type de ligne, représentant le sinus de la longitude, qui intègre pi dans l'équation.

Ce graphique montre que le mouvement longitudinal de la Lune n'est pas uniforme en raison de son orbite elliptique, mais qu'il atteint tout de même en moyenne 360 ° par mois draconique. Si ce mouvement avait été étudié avec précision, il serait apparu clairement que la Lune se déplace selon une ellipse et non un cercle.

J'ai imaginé que l'alignement ressemblait à un axe géant sur un graphique, mesurant le mois draconitique en jours et suivant la longitude au fil du temps, permettant aux observateurs de suivre quotidiennement la position de la Lune et de visualiser son mouvement, lorsqu'elle revient au même nœud après 27,2122 jours. Certaines observations ont peut-être été faites sur le segment d'un mois de la ligne, entre le premier et le deuxième dolmen, et d'autres sur une période de dix mois draconitiques, soit sur toute la ligne. La Lune effectue une révolution complète de 360° en longitude environ tous les mois sidéraux (27,3 jours), ce qui constitue une référence utile pour suivre des cycles complets. Or, lors d'un mois draconitique, la Lune revient au même nœud après environ 27,2122 jours, ce qui signifie que la longitude effectue un cycle complet de 360° par rapport aux nœuds lunaires. Les oscillations de la Lune en latitude suivent une courbe sinusoïdale, ce qui signifie que π est inhérent à la description mathématique de son mouvement. La forme fondamentale d'une onde sinusoïdale est directement liée au rapport entre la circonférence d'un cercle et son diamètre, π. Si l'orbite de la Lune était suivie à l'aide de cette méthode, π pourrait être un composant caché dans la conversion du mouvement linéaire en modèles cycliques. Bien que la longitude suive une progression plus linéaire, elle peut toujours être utile pour décrire des cycles périodiques, comme un demi-cycle représentant environ 180° (ou π radians). J'ai été intriguée par le fait que π et le nombre 360 ​​soient tous deux inclus dans la mesure, vraisemblablement les 360 représentant environ les degrés d'un cercle. Peut-être avons-nous affaire à deux manières différentes mais liées de mesurer le mouvement circulaire : un système à 360°, en degrés, reflétant le voyage de 360° en longitude environ chaque mois sidéral ou draconique, et également un système basé sur π, utilisant des radians, un système qui fonctionne bien avec le mouvement des vagues, les oscillations et le comportement sinusoïdal (comme l'oscillation de la Lune en latitude).

Ainsi, d'une part, un observateur pourrait mesurer où se trouve la lune sur son orbite, en utilisant le système à 360° pour une rotation complète, et d'autre part, le modèle ondulatoire du mouvement de la lune pourrait être suivi et exprimé en termes basés sur π (puisqu'une onde sinusoïdale complète est de 2π radians). Si le mouvement quotidien de la Lune en longitude (environ 360° / 27,2122 ≈ 13,23° par jour) équivaut à 0,231π radians par jour, son mouvement au fil du temps peut être décrit en utilisant l'un ou l'autre système. Si nous représentons graphiquement la longitude de la Lune au fil du temps, elle oscille de haut en bas en latitude selon un modèle sinusoïdal. Ceci est naturellement exprimé en utilisant π. On aurait peut-être pu placer 360 marqueurs le long de la ligne (en supposant que le sol puisse être aplani, par exemple avec une corde ou du bois), afin de cartographier les degrés de rotation d'un cycle en fonction, par exemple, de la longitude ou d'un autre aspect du mouvement de la Lune au cours d'un mois draconique. On aurait également pu tracer une fonction sinusoïdale où la longitude varie avec le temps, afin de comprendre les mouvements périodiques et de prédire les éclipses. En bref, si π et 360° apparaissent tous deux dans l'interprétation en pouces des dimensions de l'alignement, aux côtés du mois draconique en jours, l'objectif de l'alignement était peut-être de suivre les cycles lunaires et de décrire le mouvement de la Lune au cours de ce cycle, dans une sorte de graphique 3D à taille humaine.

Les graphiques ci-dessous montrent la précession nodale et l'oscillation de la latitude de la lune, qui autaient pu etre étudiés aussi.

Le rôle de la racine carrée de 10 dans le chronométrage mégalithique ?

Une caractéristique mathématique clé ressort de cette étude : le rôle de la racine carrée de 10 comme facteur proportionnel reliant les sections de l’alignement. Le premier segment du système, peut-être ancré dans le mois draconitique, les cycles d’éclipses et le cadre à 360 degrés, représenterait une structure temporelle lunaire. En multipliant par √10, ce cadre lunaire se transforme en un système basé sur l’année solaire (365 jours), avec un lien supplémentaire avec le cycle de 8 ans de Vénus et une périodicité de 800 ans. Cette relation proportionnelle suggère que les constructeurs mégalithiques ont peut-être codé un principe d’échelle géométrique permettant la conversion des mesures lunaires en cycles solaires et planétaires. Un tel système fournirait un moyen sophistiqué de suivre les rythmes célestes à long terme, intégrant potentiellement les éclipses lunaires, les phases vénusiennes et les périodicités solaires dans un modèle astronomique unifié exprimé par la géométrie du site.

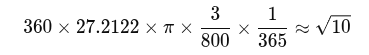
Voici deux équations clés illustrant comment la racine carrée de 10 pourrait agir comme un facteur proportionnel reliant les cycles lunaire, solaire et vénusien. En partant d'un cadre lunaire, nous pouvons considérer le produit du mois draconitique de 27,2122 jours, du système angulaire de 360° et de π :

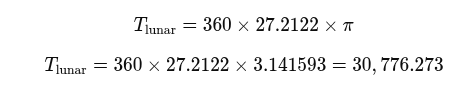
En multipliant par √10​, nous pouvons alors passer à un cadre lié au solaire :

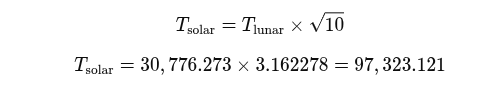
Ce nombre, 97 323,121, est proche de 800/3 x 365 et correspond à la distance entre les dolmens 1 et 3 en pouces. Le cycle de 8 ans, ou octaeteris, lié au cycle de Vénus, était un élément clé des calendriers antiques. 800 ans divisés en trois parties donnent : 800/3 = 266,667.

La période nodale (cycle complet des nœuds lunaires revenant à la même position) est de 6 798,38 jours.

Divisé par 17, le résultat est 399,905, soit près de 400. Un mois draconitique de 27,2122 jours multiplié par 49 est très proche de 4 000 / 3, et donc 49 x 3 années draconiques équivalent presque exactement à 4 000 jours. Cela confirme que la période nodale (6 798,38 jours) peut être structurée autour de multiples du mois draconitique (27,2122 jours) et des nombres 17, 49, 4 et 3. Cela suggère que la période nodale a pu être intégrée au chronométrage mégalithique grâce à l'échelle harmonique, une structure mathématique convaincante reliant les cycles lunaires et la périodicité des éclipses à long terme. Ces équations étayent l'idée que les arpenteurs et bâtisseurs mégalithiques ont utilisé l'échelle géométrique et les relations harmoniques pour unifier différents cycles célestes.

Conclusion : Un monument aux mathématiques et à l'astronomie

L'alignement de Plouharnel n'est pas seulement un exemple remarquable de topographie néolithique ; il témoigne d'une connaissance approfondie de la géométrie, de la métrologie et des cycles célestes. La présence de √10 suggère un principe géométrique intentionnel, tandis que la longueur totale de l'alignement est directement liée aux cycles lunaires et aux anciennes unités de mesure.

Les recherches de Quentin Leplat mettent en évidence la manière dont ces mégalithes s'inscrivaient dans un ensemble beaucoup plus vaste, non seulement au sein du paysage, mais aussi dans un cadre sophistiqué de mesure et d'observation astronomique. Qu'il soit utilisé comme ligne de visée pour l'observation, comme système métrologique ou comme moyen de suivi des cycles célestes, cet alignement témoigne d'un niveau de sophistication mathématique qui dépasse de loin les hypothèses communément admises sur les cultures néolithiques.

Des recherches futures devraient explorer d'autres alignements en Bretagne et au-delà, afin de vérifier si des modèles similaires existent ailleurs. Si tel est le cas, cela pourrait redéfinir notre compréhension de la science mégalithique et de ses liens profonds avec les systèmes de connaissances anciens.

Les preuves présentées dans cette étude suggèrent fortement que les dolmens de Plouharnel n'ont pas été placés au hasard, mais s'inscrivaient dans un alignement délibéré et mathématiquement structuré. L'intégration de la racine carrée de dix, des anciens systèmes de mesure et des cycles astronomiques, en particulier le mois draconique, témoigne d'une compréhension avancée de la géométrie et des mouvements célestes. Ces découvertes remettent en question les conceptions conventionnelles des sociétés néolithiques, soulignant leur potentiel de sophistication en matière de topographie, de chronométrage et d'organisation de l'espace. Des recherches interdisciplinaires plus poussées, intégrant l'archéologie, l'astronomie et la métrologie, pourraient apporter un éclairage supplémentaire sur les systèmes de connaissances des civilisations préhistoriques et leur impact durable sur l'histoire humaine.

Si vous n'avez pas encore vu le film de Quentin Leplat, « Arpenteurs du Néolithique », n'hésitez pas à le faire!

-

Notes

1. Voir Heath, Richard & Heath, Robin, 2010, "The Origins of Megalithic Astronomy as found at Le Manio " https://www.academia.edu/5384545/The_Origins_of_Megalithic_Astronomy_as_found_at_Le_Manio). Et https://www.mercurialpathways.com/post/84-the-inch-prehistoric-measure-of-time