97. Metonic Circle, Measure, and the Megalithic Yard

Le yard mégalithique, une unité proposée pour la première fois par Alexander Thom au milieu du vingtième siècle, demeure l’une des idées les plus stimulantes et controversées dans l’étude des systèmes de mesure préhistoriques. Les relevés de Thom sur les cercles de pierres à travers la Grande-Bretagne l’ont conduit à proposer l’existence d’une unité standardisée. Ses conclusions, bien que discutées, ont ouvert la voie à une réévaluation de ce que la géométrie préhistorique pouvait signifier et de la manière dont les bâtisseurs anciens pouvaient relier leurs monuments aux cycles du temps et aux phénomènes astronomiques.

Le professeur Thom aborda la question de la géométrie préhistorique avec l’esprit d’un ingénieur et la rigueur d’un géomètre. Il rassembla des milliers de mesures provenant de cercles de pierres répartis en Écosse, en Angleterre, au Pays de Galles et en Bretagne. Dans Megalithic Sites in Britain (1967) et Megalithic Lunar Observatories (1971), il conclut que « les bâtisseurs utilisaient une unité de longueur standard avec une précision notable », et que cette unité, la yard megalithique, avait une valeur de 2,72 pieds, soit 32,64 pouces ou 0,829 mètre. Thom attira l’attention sur la remarquable constance de cette mesure dans des monuments séparés par des centaines de kilomètres, affirmant que « la récurrence de cette même unité est telle que le hasard ne peut l’expliquer ».

Les expressions les plus nettes du yard megalithique apparaissent dans les cercles de pierres constitués de nombreux orthostates. Thom cita fréquemment les anneaux de Callanish et de Stenness, ainsi que le grand cercle d’Avebury et les cercles à pierre couchée du nord-est de l’Écosse. En Bretagne, il identifia la même unité dans les alignements de Carnac et dans les diamètres de plusieurs tombes à couloir. Son traitement statistique l’amena à conclure que le yard megalithique n’était « pas une simple approximation commode mais un étalon délibéré », subdivisé en quarante ou cinquante parties égales. Bien que l’analyse de Thom soit largement ignorée aujourd’hui, l’ensemble de données demeure impressionnant. La récurrence de la valeur proposée par Thom, tant dans les monuments britanniques que français, fait que le yard megalithique continue d’être sérieusement envisagé, en particulier lorsqu’on l’examine en relation avec les cycles astronomiques plutôt qu’avec des dimensions architecturales isolées. La question demeure donc ouverte : le yard megalithique encode-t-il une forme de réconciliation entre temps solaire et temps lunaire par une géométrie circulaire ?

Le cycle métonique

Plusieurs rapports entre années solaires ou tropicales et mois lunaires synodiques permettent des concordances relativement précises. Le cycle métonique est l’un de ces rapports. Il correspond à dix-neuf années de 365,242199 jours, ou à 235 mois lunaires synodiques de 29,53059 jours. Il concilie également le mois sidéral de 27,321661 jours avec ces deux autres périodes. Ainsi :

235 × 29,53059 ≈ 19 × 365,242199 ≈ 254 × 27,321661

Le cycle métonique fut employé dans l’Antiquité, et quatre cycles métoniques réunis, formant le cycle callippique, en amélioraient encore la précision. Le cycle métonique fut notamment intégré au célèbre mécanisme d’Anticythère, un dispositif grec du deuxième siècle avant notre ère destiné à calculer les positions planétaires et lunaires. Ce mécanisme reposait sur la fraction 254 / 19 pour modéliser le cycle métonique.

La fraction 254/19 dans le mécanisme d’Anticythère

Le mécanisme d’Anticythère, retrouvé dans l’épave d’un navire du premier siècle avant notre ère, est la plus ancienne machine astronomique à engrenages connue. Elle incorpore dans ses rouages le rapport 254/19, une fraction utilisée pour approximer le cycle métonique.

Les analyses modernes, en particulier celles de Freeth, Jones et de leurs collaborateurs, ont montré que l’indicateur métonique du mécanisme est entraîné par une chaîne d’engrenages construite autour de la relation entre les cycles lunaires et solaires. Pour reprendre les termes de Freeth et al. dans Nature (2006) :

Ce rapport constitue une approximation entière très efficace de la relation plus exacte entre 235 lunaisons et 19 années solaires, permettant au mécanisme de faire avancer son calendrier lunaire à un rythme correct, sans recourir à des nombres irrationnels.

La présence répétée du cycle de dix-neuf ans, le même qui régit votre modèle de cercle métonique, montre à quel point le système métonique se trouvait au cœur de la pratique astronomique antique.

On trouve le rapport 254/19 au sein du mécanisme sous la forme d’un engrenage dédié : chaque rotation du pointeur solaire entraîne l’avancement exact du disque calendaire lunaire. Le dispositif d’Anticythère constitue ainsi un témoignage hellénistique indépendant attestant l’usage du ratio métonique comme principe structurant dans la conception astronomique.

Le rapport 19/254

En inversant ce rapport, 19 / 254, et en l’appliquant à la géométrie du cercle et au mètre, on obtient un indice possible de ce que pourrait représenter le yard mégalithique. Le yard mégalithique peut être interprété comme la circonférence d’un cercle de dix neuf mètres de diamètre, divisée en soixante douze parts égales. Cela donne une valeur de 32,639 pouces lorsque l’on emploie la valeur de π fournie par les calculateurs modernes. Exprimé en mètres, 19π/72 donne 0,82903, une valeur qui n’est pas très éloignée de l’expression métrologique 12⁴ × 4/100 000 mètres. Le choix d’un cercle de dix neuf mètres de diamètre présente l’avantage d’ancrer l’unité de mesure dans un cadre astronomique, ce qui s’accorde bien avec l’idée selon laquelle de nombreux monuments mégalithiques étaient conçus en relation avec les cycles célestes.

La division de la circonférence en soixante douze parts égales évoque non seulement des nombres harmoniques mais aussi des subdivisions précessionnelles, telles que celles dérivées du cycle de vingt cinq mille neuf cent vingt ans. Ainsi, cette lecture du yard mégalithique ne l’isole plus comme une simple unité de chantier ou une abstraction mathématique arbitraire, mais l’inscrit au contraire dans une trame conceptuelle où géométrie, mesure du temps et observation astronomique se trouvent intimement reliées.

Pour obtenir la valeur du yard mégalithique en pouces, c'est-à-dire pour convertir l'équation ci-dessus de mètres en pouces, il faut multiplier par 100 000 / 254.

19/254 π x 100 000 / 72 = 32,639 pouces.

Comme indiqué précédemment, 254 correspond au nombre de mois sidéraux dans une période métonique. Et 19/254 rappelle le rapport 254/19 présent dans le mécanisme d'Anticythère.

Ceci suggère que le mètre, le pouce et le yard mégalithique sont liés à l'astronomie, dans un contexte préhistorique, et plus particulièrement au cycle métonique, ainsi qu'à la nécessité de concilier les cycles du soleil et de la lune. Si l'on considère le mètre comme une unité de mesure fondamentale, le yard mégalithique peut être compris comme le produit de cette unité et de la géométrie du cercle au sein d'un dessein cosmique plus vaste. 19π / 72 équivaut à 0,82903 mètre, une valeur étonnamment proche des 0,829 m de Thom. Le mètre, une rationalisation de la circonférence polaire terrestre, fournit le cadre géométrique nécessaire pour tenter de lier le rythme céleste à la forme terrestre par le biais des nombres, des proportions et de la géométrie. Le pouce introduit le nombre 254 dans l'équation, la reliant au cycle métonique via le mois sidéral.

La logique lunaire et solaire sous-jacente au mètre et au pouce

Si le mètre représente approximativement la circonférence polaire, soit environ un quatre-millionième de celle-ci, le pouce représente approximativement la circonférence équatoriale. Cette intuition a été, à ma connaissance, proposée pour la première fois par Robyn Heath dans *The Lost Science of Measuring the Earth*, ouvrage coécrit avec John Michell. Selon lui, la circonférence peut être comprise comme 365,25 x 360 000 pieds anglais (ou 365,242199 x 360 000 pieds). Une autre façon d'exprimer le lien entre le pouce et la circonférence polaire est par le biais de la période de 4 320 000 ans appelée yuga dans la tradition indienne. La circonférence devient alors 4 320 000 x 365,25 pouces (ou 4 320 000 x 365,242199 pouces). Un point situé sur l'équateur parcourt donc 4 320 000 x 365,25 pouces en 365,25 jours, par rapport à l'axe de la Terre (et non par rapport aux étoiles ou au Soleil).

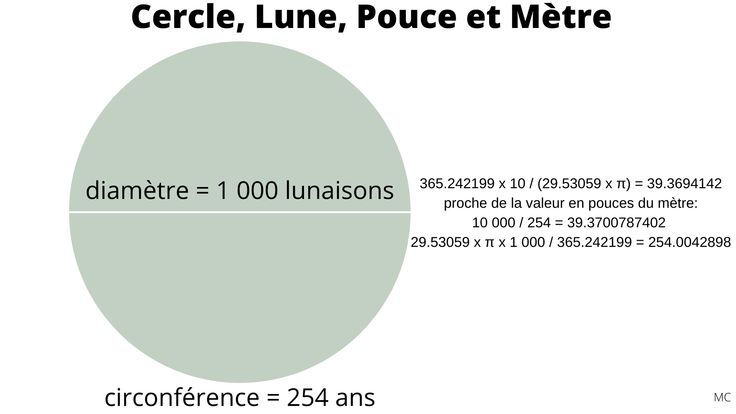
La division de la circonférence équatoriale en 4 320 000 x 365,25 parties et celle de la circonférence polaire en 40 000 000 parties se concilient par la géométrie du cercle et la concordance des cercles solaire et lunaire grâce au cycle métonique. Par une étrange coïncidence, un cercle de diamètre 1000 x 29,53059 a une circonférence très proche de 254 x 365,242199 unités (29,53059 étant le mois synodique en jours et 365,242199 l'année solaire en jours). Ainsi, lorsque le diamètre du cercle est fixé à mille mois synodiques, exprimés en jours, la circonférence correspond presque exactement à 254 années solaires, également exprimées en jours, en utilisant le nombre pi. Pi semble ainsi unifier les nombres métoniques. 19 est le nombre d'années, 254 le nombre de mois sidéraux et 235 le nombre de mois synodiques.

19π × 1000 / 254 = 235,001

29,53059 × π ​​× 1000 / 365,242199 ≈ 254

365,242199 × 10 / (29,53059 π) ≈ 39,37

Ce nombre de 39,37 correspond au nombre de pouces dans un mètre, une valeur si proche qu'elle suggère un lien délibéré entre le cycle lunaire, l'année solaire et l'interaction entre le diamètre et la circonférence d'un cercle (π).

Si l'on trace un cercle de 35,436708 mètres de diamètre, sa circonférence est de 365,24836 pieds impériaux, soit approximativement la durée d'une année solaire. Cette géométrie fait écho à l'équation solaire et lunaire :

365,24836 / π = 35,436708

 Il existe un ensemble intéressant de relations numériques qui apparaissent lorsqu'on compare la structure du mètre avec le comportement des cycles lunaires et solaires. Si l'on prend le dix-millième du quadrant polaire, soit mille mètres, et qu'on le multiplie par la durée de l'année lunaire exprimée en jours (354,36) et par la valeur de pi, puis qu'on divise le résultat par 254 et par 12, on obtient 365,24107, une valeur très proche d'une année en jours. On obtient la même valeur en divisant le quadrant polaire par cent millions pour obtenir un dixième de mètre, puis en multipliant par 354,36 et par pi : le résultat est à nouveau 365,24107, exprimé cette fois en pieds. Une autre variante, où le quadrant polaire est divisé par cent mille, multiplié par la durée de l'année lunaire et par pi, puis par 360, donne un résultat proche de la circonférence équatoriale exprimée en mètres.

Si l'on divise le quadrant polaire par 10⁵, que l'on multiplie par le nombre de jours d'une année lunaire (354,36), par π et par 360, on obtient une très bonne approximation de la circonférence équatoriale de la Terre en mètres.

Circonférence équatoriale ≈ Quadrant polaire × année lunaire × 360 × π / 10⁵

Par définition, le quadrant méridien mesure 10 millions de mètres, bien que les estimations suggèrent une légère marge d'erreur. En tenant compte de l'année lunaire et de l'angle d'un cercle complet, le même quadrant polaire donne, de manière quasi exacte, la circonférence équatoriale en mètres.

Le méridien polaire, divisé en quelque 40 millions de parties pour produire le mètre, et l'équateur, divisé en quelque 4 320 000 × 365 pouces, sont alors les deux faces d'un même schéma, harmonisées par des facteurs tels que 354,36 et 254, qui relèvent de la réconciliation du temps solaire et lunaire dans la tradition métonique. Dans cette perspective, le mètre et le pouce ne sont pas des unités rivales issues de deux systèmes de mesure historiques, mais des expressions jumelles d'un même schéma. La géométrie offre un moyen naturel de réconcilier les cycles du soleil et de la lune. Ces deux unités peuvent donc être interprétées comme des longueurs calendaires, émergeant d'une vision du monde où nombre, astronomie et géométrie forment un tout cohérent. C'est dans cet univers intellectuel que semblent participer le cycle métonique, le yard mégalithique et des mécanismes tels qu'Anticythère.

On peut se demander si la valeur du yard mégalithique exprimée en pieds, soit 2,72, sert à encoder le mois draconique de 27,2122 jours. Si cette ressemblance est intentionnelle, même approximative, elle situerait le yard mégalithique parmi les constantes lunaires qui structurent la géométrie des éclipses. Une longueur évoquant le cycle draconique serait un choix délibéré pour tout système visant à concilier le temps solaire et le temps lunaire, car le mois draconique régit les points où la trajectoire de la Lune croise l'écliptique et détermine ainsi la période des éclipses. Que cet écho soit le fruit d'une conception numérique ou un simple effet secondaire de l'utilisation de soixante huitièmes d'un cercle de dix-neuf mètres, il renforce l'impression que le yard mégalithique, quelle que soit son origine exacte, se situe à la croisée de la géométrie et des cycles célestes, et que sa simplicité apparente recèle une signification astronomique profonde.

Dans l'excellent ouvrage de Geoff Bath, Stone Circle Design and Measurement, Standard Units and Complex Geometries, figure un tableau répertoriant les diamètres, en mètres, des nombreux cercles étudiés par l'auteur. Un seul atteint 19 mètres de diamètre : Yonder Bognie, en Écosse. Merrivale SE, quant à lui, mesure 19,1 mètres de diamètre. On observe une grande variété de dimensions pour les cercles de pierres en général, avec quelques valeurs récurrentes, comme 3,1 et 3,2 mètres, ou encore 31,5 et 31,6 mètres de diamètre. En revanche, aucun cercle de 19 mètres de diamètre ne semble se répéter. Curieusement, si le diamètre était en réalité de 3,101 mètres, les cercles de 3,1 mètres auraient une circonférence de 235/20 pouces. Or, 235 correspond au nombre de mois synodiques dans une période métonique. Il est donc possible que le diamètre de 3,1 mètres, présent dans 11 cercles du tableau de Geoff Bath, ait également un lien métonique.

 La juxtaposition des découvertes de Thom avec le cadre métonique offre une perspective d'interprétation intéressante, quoique spéculative. Si le yard mégalithique représente la division d'un cercle de 19 mètres de diamètre en soixante-douze parties, alors la découverte empirique de Thom peut être comprise non pas comme une simple commodité de construction, mais comme une abstraction géométrique de la réconciliation entre l'année lunaire et l'année solaire. Le yard mégalithique devient ainsi un pont entre le mouvement céleste et l'échelle humaine, entre les cycles du ciel et les mesures de la terre. Il est donc raisonnable de considérer le yard mégalithique comme un quantum de mesure luni-solaire, issu des mêmes harmonies mathématiques qui ont donné naissance au pouce et au mètre.

Bibliographie

Bath, Geoff. Stone Circle Design and Measurement, Standard Units and Complex Geometries 2: Stylised Plans and Analysis of over 300 Rings. Key Press, UK, 2021.

Chamberlain, Andrew & Pearson, Mike Parker. “Units of Measurement in Late Neolithic Southern Britain.” In Larsson, M. & Parker Pearson, M. (eds) From Stonehenge to the Baltic: Living with Cultural Diversity in the Third Millennium BC, BAR International Series 1692. Archaeopress, Oxford, 2007, pp. 169–174.

Heath, Robin & Michell, John. The Lost Science of Measuring the Earth. Adventures Unlimited Press, 2006

Thom, Alexander. Megalithic Sites in Britain. Oxford University Press, 1967.

Thom, Alexander & Thom, Archie. Megalithic Remains in Britain and Brittany. Clarendon Press, Oxford, 1988.

Freeth, Tony, et al. “Decoding the Ancient Greek Astronomical Calculator Known as the Antikythera Mechanism.” Nature 444 (2006): 587–591.